Experimentant amb la funció quadràtica

La funció quadràtica és abastament estudiada en els darrers cursos de la secundària obligatòria. Són molts els exemples i experimentacions que s’han emprat per tal de treballar-la; a tall d’exemple tenim els llançaments a cistella i la modelització de la seva trajectòria. En aquesta pràctica partirem de la corba que ens dóna la funció $f(x)=x^2$ i en un procés de recerca guiat en funció de l’edat del nostre alumnat, descobrirem propietats i aplicacions interessants. Per tal d’ajudar-nos en aquest procés he construït alguns applets en GeoGebra perquè la seva manipulació faciliti la cerca de conclusions. Evidentment, el professor pot incloure com a treball la realització d’aquestes construccions o similars per part dels alumnes; i és que no cal oblidar que aprenem fent.

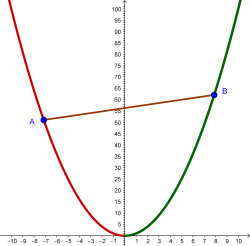
Considerem la gràfica de la funció $f(x)=x^2$ . La recta vertical $x=0$ , l’eix d’ordenades, ens divideix la paràbola en dos trossos simètrics. Prenem un punt qualsevol de cadascuna de les branques tal i com es mostra en la figura 1.

figura 1

figura 2

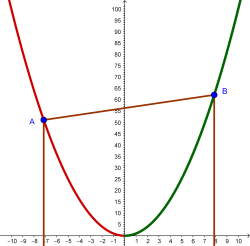
Si unim aquests punts el segment resultant ens tallarà l’eix a una altura determinada (figura 2). Marquem el punt de tall entre el segment $\overline{AB}$ i l’eix d’ordenades, i tracem dues semirectes amb origen els punts triats i direcció $\overrightarrow{(0,-1)}$ .

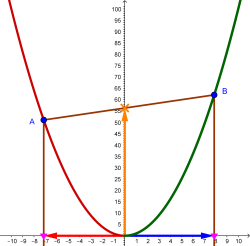
Existeix alguna relació entre les distàncies a les que es troben cadascun dels punts $A$ i $B$ a l’eix d’ordenades i l’altura obtinguda per la intersecció del segment $\overline{AB}$ amb l’eix $x=0$ ?

Les figures següents il·lustren la situació plantejada.

figura 3

figura 4

Desplacem els punts $A$ i $B$ de l’applet de GeoGebra per tal de donar-ne una resposta.

Pot ser interessant discutir-ho en grup i fer-ne una posada en comú. Per això cal assegurar-se’n de no desplaçar del no al sí el punt lliscant que hi apareix fins que no s’hagi manipulat i discutit suficientment la construcció.

Sorprenent, oi? Ens trobem davant d’una màquina de multiplicar! La podem emprar per a fer multiplicacions o divisions de nombres reals. Alhora també ens serveix per determinar parelles de nombres tals que el seu producte sigui igual a un ja donat anteriorment. Si seleccionem la Pràctica 2 de l’applet de GeoGebra veurem com la màquina ens pot ser útil per estudiar situacions com les següents:

Troba dos nombres que multiplicats doni 30. Quants en podem trobar?
Si dibuixem en uns eixos de coordenades el conjunt de valors (x,y) de manera que x·y=30, què obtenim?
I si en lloc de 30 és un altre valor qualsevol, a quines conclusions arribem?

imatge de la pràctica portada a 2n d’ESO

Construcció

Pot resultar un bon projecte la construcció física de l’aparell.

Recomano una planxa metàl·lica de $50\, \times \, 50\ [cm^2]$ , un metre i mig de cordill, dos imants de neodimi amb ganxos, dos pesos i la funció quadràtica dibuixada en uns eixos de coordenades amb els nombres ben marcats.
[us podeu descarregar i imprimir aquestes plantilles: sencera / en 4 trossos]

Imprimirem la funció quadràtica i la muntarem de manera que tingui les mides de la planxa.
Els dos imants amb ganxos seran els dos punts de la paràbola.
Farem passar el cordill pels dos ganxos i per finalitzar, lligarem els pesos als extrems del cordill. D’aquesta manera aconseguirem que estigui ben tensat.

Demostració

A partir de tercer o quart de secundària podem plantejar als nostres alumnes que intentin demostrar la propietat trobada. D’aquesta manera treballarem els conceptes de raó, semblança, proporcionalitat, el Teorema de Tales, identitats notables, etc.

En la següent construcció de GeoGebra es pot seguir la demostració.

I si fem un pas al 3D?

La pregunta que ens sorgeix ara és què succeirà si treballem en 3 dimensions?

Aquest pot resultar un bon exercici per a les classes de batxillerat. Per respondre aquesta i d’altres preguntes que s’esdevenen, seguirem les instruccions de l’applet i estudiarem de forma ordenada els tres casos que es presenten.

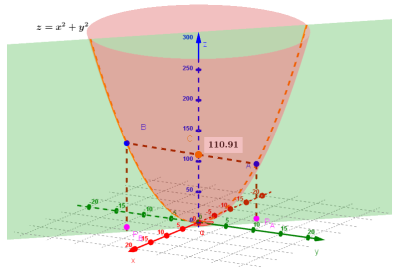
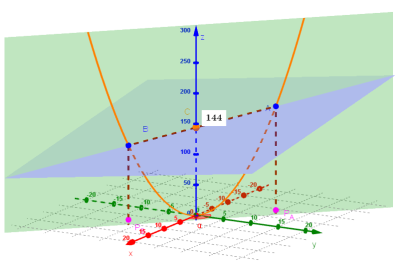
En el cas 1 observem com la paràbola és obtinguda a partir de la intersecció del paraboloide $z=x^2+y^2$ i un pla que conté l’eix z (pla 1).

Activant i desactivant les respectives caselles de control veurem la construcció.

Prenent dos punts, $A$ i $B$ , sobre aquesta paràbola i unint-los, el segment que determinen interseca l’eix z en el punt “producte” $C$ en el mateix sentit que abans ho fèiem en 2D. El producte de les distàncies respectives des d’aquests punts a l’eix z ve donat pel valor on el segment $\overline{AB}$ talla l’eix. Talment podem reproduir aquesta idea per a les infinites paràboles que s’obtindrien si considerem el feix de plans que conté l’eix z. Ho podem observar desplaçant el punt lliscant $\alpha$ .

figura 5

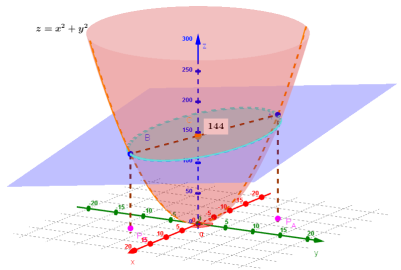
Ara bé, i si fixem el valor del producte? És a dir, podríem donar un determinat valor de l’eix z i estudiar quines parelles de punts de les paràboles verifiquen la relació estudiada. Aleshores, considerem un segon pla perpendicular al pla 1 i que contingui el punt $C$ . Quants plans existeixen amb aquestes condicions? Un nou feix! Cadascun d’aquests ens determina la parella de punts que busquem quan interseca amb la paràbola. Tot això ho podrem observar en el cas 2.

figura 6

La investigació continua i, si tenim activades les caselles de control paraboloide i pla 2, veurem que aquests intersequen en una el·lipse amb eix major el segment $\overline{AB}$ .

figura 7

Es pot veure com totes les parelles de punts de l’el·lipse que units formen un segment que passa per $C$ compleixen que el producte de les seves distàncies a l’eix z és igual a l’altura de $C$ .

figura 8

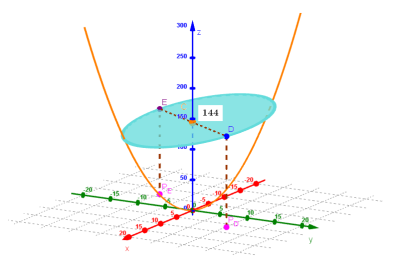
Activant l’opció del cas 3 finalitzarem la generalització d’una petita investigació que començava manipulant dos punts sobre la gràfica de $f(x)=x^2$ .

Consideracions/recomanacions per dur-la a l’aula

Considero que aquesta pot resultar una pràctica interessant de centre ja que es pot portar a l’aula en diferents cursos per treballar temes propis del currículum.
Els alumnes del cicle superior de Primària o del primer cicle de l’ESO poden realitzar perfectament la seva construcció i, d’aquesta manera utilitzar-la a les classes com a màquina multiplicadora. És molt útil per fer estimacions de càlculs:

Donats dos nombres qualssevol entre 0 i 10 estimar quin serà el seu producte.
Donat un nombre entre 0 i 100, i un altre entre 0 i 10 estimar quin serà el quocient del primer respecte el segon nombre.
Donat un nombre entre 0 i 100 estimar quina seria la seva arrel quadrada.

Un altre aspecte interessant per treballar a 1r i 2n d’ESO és expressar un nombre com a producte de dos altres, i aquests últims expressar-los com un parell ordenat.
Per exemple, donat el nombre 30 les primeres parelles que surten, si es planteja el dubte a tota la classe, són (1,30) (2,15) (3,10) (6,5). Si els representem en uns eixos de coordenades provoquem que també surtin les parelles (5,6) , (10,3) , (15,2) i (30,1) repassant d’aquesta manera la propietat de commutativitat del producte.
Cal forçar un xic més perquè entre tots surti que les parelles (-1,-30), (-2,-15), …. també serien solució del problema plantejat.
La descoberta per a ells esdevé quan se n’adonen que hi ha infinites parelles de nombres que multiplicades donen 30… i això és espectacular. La discussió en petits grups i la posada en comú facilitarà aquestes petites descobertes. Tanmateix, la manipulació dels applets de GeoGebra presentats anteriorment també podrien ajudar.

Al segon cicle de l’ESO podem portar l’activitat per treballar la funció de proporcionalitat inversa, la funció quadràtica i la propietat multiplicadora que té aquesta última. Reforçaríem els conceptes de funció, imatge i antimatge, intersecció entre dues corbes, identitats notables, hipèrbola, equacions de la recta, proporcionalitat, raó, semblança, Teorema de Tales,…

A 1r de Batx l’activitat entra amb més força ja que, a part dels punts anteriors, podem treballar l’expressió del feix de rectes que passa per un punt, la paràbola, la hipèrbola i l’el·lipse com a còniques. També pot ser convenient proposar que construeixin en grups applets de GeoGebra sembants als proposats i que els permetin visualitzar les hipòtesis que es fan.

El pas a 3D jo el proposo per a 1r de batxillerat (la visualització) i per a 2n de batx (la construcció). Ens serà útil per treballar equacions de plans, feixos de plans secants, plans ortogonals, interseccions entre plans, …

Per descomptat ens trobem davant d’una activitat de LABORATORI DE MATEMÀTIQUES.

Nivell:	internivells
Tema:	investigacions
Autoria:	Manel Martínez i Pascual